Factors of 110—with Easy division and prime factorization
Contents
Factors of 110
When you multiply two consecutive numbers 10 and 11, you get 110. For a better understanding, we will calculate the factors of 110, prime factors of 110, and factors of 110 in pairs along with solved examples.
Factors of 110: 1, 2, 5, 10, 11, 22, 55 and 110
Prime Factorization of 110: 110 = 2 × 5 × 11
What are the Factors of 110?
The factors of 110 are the numbers multiplied in pairs to give the result of 110. Those factors that divide 110 without leaving any remainder are the factors of 110. Therefore, when you multiply two whole numbers with each other and get 110 as the answer, you can say that both those numbers are factors of 110.
Take note of the following numbers. When you multiply the given numbers, you get 110.
1 × 110 = 110
2 × 55 = 110
5 × 22 = 110
10 × 11 = 110
11 × 10 = 110
22 × 5 = 110
55 × 2 = 110
110 × 1 = 110
Therefore, we can say that “The factors of 110 are all the integers that can be divided by 110.”
What are the Factors of -110?
When we multiply two numbers, and we get -110 as a product, those numbers are the factors of -110.
Here is the explanation:
-1 × 110 = -110
1 × -110 = -110
-2 × 55 = -110
2 × -55 = -110
-5 × 22 = -110
5 × -22 = -110
-10× 11 = -110
10 ×-11 = -110
We can get -110 by having (-1, 110), (-2, 55), (-5, 22), and (-10, 11) as a pair of factors. Similarly, we can also get -110 by having (1, -110), (2, -55), (5, -22), and (10, -11) as a pair of factors.
How to Calculate the Factors of 110?
Start by calculating the factors of 110, starting with the smallest whole number, i.e., 1.
Divide 110 by this number. Is there a remainder of 0?
Definitely! This is what we get
110/1 = 110
110 × 1 = 110
2 is the next whole number
Divide 110 by this number.
110/2 = 55
2 × 55 = 110
In a similar fashion, we get
110 = 1 × 110 = 2 × 55 = 5 × 22 = 10 ×11
The factors of 110 are as follows:
Therefore, the factors of 110 are 1, 2, 5, 10, 11, 22, 55, and 110.
Using interactive examples and illustrations, explore factors.
Factors of 112—The factors of 112 are 1, 2, 4, 7, 8, 14, 16, 28, 56, 112
Factors of 108—The factors of 108 are 1, 2, 3 , 4, 6, 9, 12, 18, 27, 36, 54, 108
Factors of 50—The factors of 50 are 1, 2, 5, 10, 25, 50
Factors of 125—The factors of 125 are 1, 5, 25, 125
Factors of 15—The factors of 15 are 1, 3, 5, 15
Factors of 100—The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100
Factors of 110 by Prime Factorization
“Prime factorization” is the process of expressing a composite number as the product of its prime factors. We can determine the prime factorization of 110 by dividing it by its smallest prime factor, which is 2.
- 110/2 = 55
Using the smallest prime factor, 55 is divided by the quotient. This process continues until we get a quotient of 1.
Here is 110’s prime factorization:
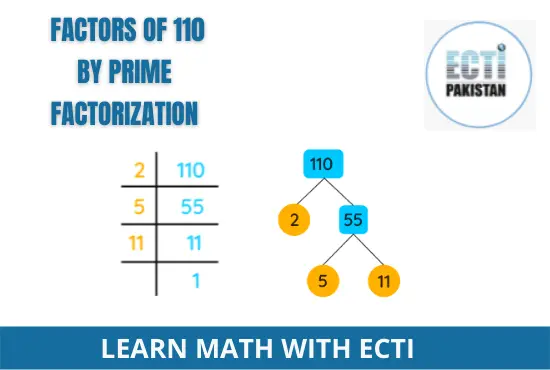
Therefore, the prime factors of 110 are 2, 5, and 11.
Factors of 110 in Pairs
Factor pairs of 110 are the pairs of numbers that give 110 when multiplied. Look at the following factors of 110 in pairs. According to the table above, no new factors are introduced after 10 × 11. Therefore, it is sufficient to find factors up until (10,11).
In the case of negative integers, both the numbers in the pair factors will be negative. Due to the fact that (- ve * – ve) = +ve, we can list the factor pairs of 110 as (-1, -110); (-2, -55); (-5, 22); and (-10, 11).
Important Notes:
Since 110 ends with the digit 0, it has the factors 5 and 10. All numbers ending with 0 have these factors as well
There are no perfect squares in 110. Thus, it will have an even number of factors. This property applies to every non-perfect square number.
Solved examples
1. Example 1:
Ali bought two rectangular rugs which had different dimensions but had the same area of 110 inches². He wanted his friend Nadeem to guess the dimensions of the rugs. Could you help him with the two probable pairs other than (1,110) and (55, 2), that would result in the given area?
Solution:
Nadeem told that (5, 22) and (10,11) were the two-factor pairs of 110 which could be the dimensions of the two rugs. Let us see how he explained it.
Since Area of a rectangle = length × breadth
For the first rug,
Area = 22 × 5 = 110 in²
For the second rug,
Area =10 × 11= 110 in²
Hence, the two-factor pairs are (22, 5) and (10, 11).
Example 2:
Ali’s teacher told him that -55 is one of the factors of 110. Can you help him find the other factor?
Solution:
110 = Factor 1 × Factor 2
Therefore, 110 =(-55) × Factor 2
Factor 2 = 110/(-55) =(-2)
Thus, the other factor is -2
| Link Related Factors | ||
| Factors of 30 = 1,2,3,5,6,10,15 and 30. | 24 factors math = 1, 2, 3, 4, 6, 8, 12 and 24. | Prime factorization of 34 = 1,2, 17, and 34. |
| Factors of 36 = 1,2,3,4,6,9,12,18, and 36. | Factors of 38= 1, 2, 19, 38. | Factors of 42 = 1, 2, 3, 6, 7, 14, 21, and 42. |
| Factors of 45 = 1, 3, 5, 9, 15, and 45. | Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | 55 factors math = 1, 5, 11 and 55. |
| Factors of 50 = 1, 2, 5, 10, 25, 50. | Factors of 54 = 1, 2, 3, 6, 9, 18, 27 and 54. | 120 factors math = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120. |
FAQ’S
What are the prime factors of 110?
There are three prime factors of 110: 2, 5, and 11.
What is the GCF of 110 and x120?
The greatest common factor between two or more numbers is called the GCF. In the case of 110 and 120, the GCF will be 10.
Which is the smallest prime factor of 110?
110 has a prime factor of 2 as its smallest.
Which is the largest prime factor of 110?
11 is the largest prime factor of 110.
What are the common factors of 110 and 140?
Factors of 110 include 1, 2, 5, 10, 11, 22, 55, and 110. There are 140 factors: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140.
Therefore, 1, 2, 5, and 10 are the common factors of 100 and 140.