Factors of 12 – Prime Factors & Pairs Factors

Contents
Factors of 12
Factors of 12 are the pairs of numbers multiplied together, resulting in the original number.
It cannot be a decimal or fraction, but it can be a pair factor of 12.
For example:
There are three possible pair factors for 12: (1, 12), (2, 6), and(3, 4).
In math, It is possible to find the factors of a number using the division method as well as the prime factorization method.
We will explore the factors of 12 in this article, as well as pair factors and prime factors of 12 by the prime factorization method with solved examples.
What are the Factors of 12?
Factors of 12 are the numbers that divide 12 exactly without leaving anything behind. The number 12 is an even composite number, so it has many factors besides 1 and 12. These factors can be positive or negative.
Therefore, factors 12 are 1, 2, 3, 4, 6, and 12.
Similarly, the negative factors of 12 are -1, -2, -3, -4, -6 and -12.

| Factors of 12: 1, 2, 3, 4, 6, and 12.Prime Factorization of 12: 2×2×3 or 22 × 3 |
What are the Factors of -12?
When we multiply two numbers and get -12 as a product, those numbers are the factors of -12. Here is the explanation:
-1 × 12 = -12
1 × -12 = -12
-2 × 6 = -12
2 × -6 = 12
-3 × 4 = -12
3 × -4= -12
We can get -12 by having (-1, 12), (-2, 6), and(-3, 4) as a pair of factors. Similarly, we can also get -12 by having (1, -12), (2, -6), and(3, -4) as a pair of factors.
Pair Factors of 12
The pair factor of 12 occurs when two numbers are multiplied together, resulting in the original number 12. Positive and negative pair factors of 12 exist both.

Here are the positive and negative pair factors of 12:
Positive Pair Factors of 12:
| Positive Factors of 12 | Positive Pair Factors of 12 |
| 1 × 12 | (1, 12) |
| 2 × 6 | (2, 6) |
| 3 × 4 | (3, 4) |
Negative Pair Factors of 12:
| Negative Factors of 12 | Negative Pair Factors of 12 |
| -1 × -12 | (-1, -12) |
| -2 × -6 | (-2, -6) |
| -3 × -4 | (-3, -4) |
Factors of 12 by Division Method
In this method, 12 can be divided by different integers to calculate its factors. When the integer divides 12 and leaves 0 in the remainder, then those integers are factors of 12.
Let’s look at the factors of 12 using the division method.
- 12/1 = 12 (Factor is 1 and remainder is 0)
- 12/2 = 6 (Factor is 2 and remainder is 0)
- 12/3 = 4 (Factor is 3 and remainder is 0)
- 12/4 = 3 (Factor is 4 and remainder is 0)
- 12/6 = 2 (Factor is 6 and remainder is 0)
- 12/12 =1 (Factor is 12 and remainder is 0)
Therefore, the factors 12 are 1, 2, 3, 4, 6, and 12. Whenever the numbers other than 1, 2, 3, 4, 6, and 12 divide 12, 12 is not divided exactly, leaving the remainder.
Prime Factorization of 12
In prime factorization, the number 12 is expressed as the product of its prime factors.
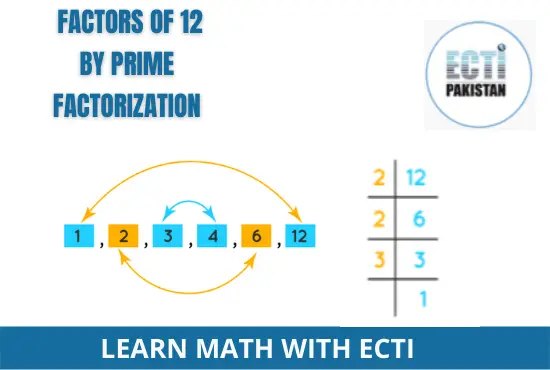
Here is the process for finding the prime factors of 12:
Let’s consider the pair factor (1, 12).
Here, 1 is neither prime nor composite. So, leave the number as it is.
Take the other number in the pair factor (12). 12 can be further factored into its prime factors since it is a composite number.
Therefore, 12 can be written as the product of 2, 2, and 3, as both 2 and 3 are prime factors.
Hence, 12 = 2×2×3
Therefore, the prime factorization of 12 is 2×2×3 or 22 × 3
Note:
In a pair factor, if a number is a prime number, leave it as it is. Where there is a composite number, its prime factors are written as a product.
Solved Examples
Example 1:
Find the common factor between 12 and 24.
Solution:
The factors 12 are 1, 2, 3, 4, 6, and 12.
All Factors of 24= 1, 2, 3, 4, 6, 8, 12, and 24.
Thus, 12 and 24 have common factors of 1, 2, 3, 4, 6, and 24.
Example 2:
Calculate the common factors of 12 and 13.
Solution:
Factors of 12 = 1, 2, 3, 4, 6 and 12.
All Factors of 13= 1 and 13.
Thus, the common factor of 12 and 13 is 1.
Example 3:
Find out the common factors of 12 and 27.
Solution:
The factors 12 are 1, 2, 3, 4, 6, and 12.
All Factors of 27= 1, 3, 9, and 27.
Therefore, the common factor of 12 and 27 is 1 and 3.
| Links Related to Factors | |
| All Factors 24= 1, 2, 3, 4, 6, 8, 12, and 24. | All Factors 13= 1 and 13. |
| Factors of 48= 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | Factors of 18= 1, 2, 3, 6, 9 and 18. |
| Factors of 42= 1, 2, 3, 6, 7, 14, 21, and 42. | Factors of 60= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. |
| Factors of 35= 1, 5, 7, and 35. | Factors of 72= 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72. |
| Factors of 84= 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84. | All Factors 55= 1, 5, 11, and 55. |
FAQ’s
What are the factors of 12?
The factors 12 are 1, 2, 3, 4, 6, and 12.
What is the prime factorization of 12?
2×2×3 or 22×3 are the prime factors of 12.
Write down the positive pair factors of 12.
The positive pair factors of 12 are (1, 12), (2, 6), and (3, 4)
Write down the negative pair factors of 12.
The negative pair factors of 12 are (-1, -12), (-2, -6) and (-3, -4).
Is 6 a factor of 12?
In fact, 6 is a factor of 12. Since 6 divides 12 exactly without leaving a remainder, 6 is a factor of 12.
