Factors of 21 – How to Find with Prime Factorization

Contents
Factors OF 21
A factor of 21 is the result of multiplying a pair of factors to give the result of 21. Factors divide the numbers uniformly.
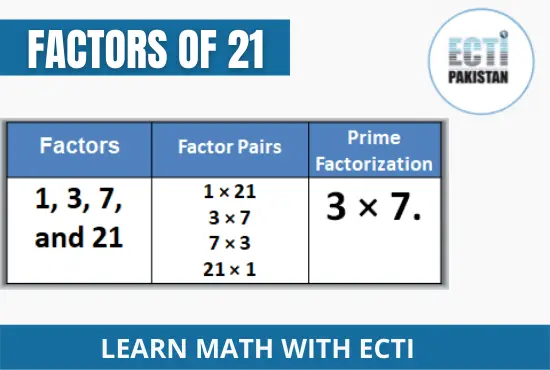
The factors of 21 are 1, 3, 7, and 21.
When these numbers are multiplied together, they give the number 21. We can use the factorization method to find the factors of the number 21.
How to Find the Factors of 21?
To find the factors of 21, follow the steps below.
Start by writing the number 21
Find the two numbers, say 3 and 7, which result in 21 when multiplied, such that 3 × 7 = 21.
It is known that 3 and 7 are prime numbers with just two factors, the number itself and one.
The factors of 3 = 3 × 1
Factors of 7 = 7 x 1
Therefore, we can’t further factorize them.
As a consequence, the factorization of 21 can be expressed as 21 = 3 × 7 × 1
Finally, list all the unique numbers obtained through the above process.
Factors of 21:
1, 3, 7, and 21
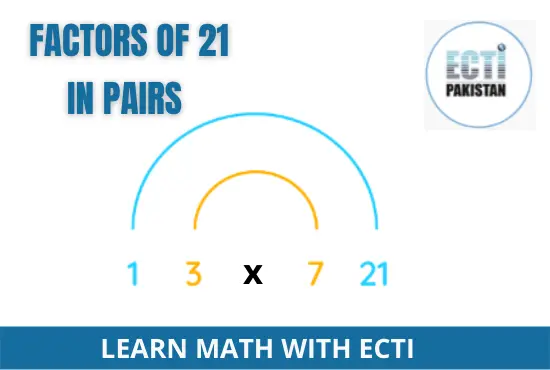
Pair Factors of 21
If you want to know the factors of 21, multiply the two numbers to get the original number. Both positive and negative integers can be written as pairs as follows:
| Positive pairs | Negative pairs |
| 1 × 21 = 21; (1, 21) | (-1) × (-21) = 21; (-1, -21) |
| 3 × 7 = 21; (3, 7) | (-3) × (-7) = 21; (-3, -7) |
| 7 × 3 = 21; (7, 3) | (-7) × (-3) = 21; (-7, -3) |
| 21 × 1 = 21; (21, 1) | (-21) × (-1) = 21; (-21, -1) |
Consequently, (1, 21), (3, 7), (7, 3), and (21, 1) are the positive pair factors of 21.
In addition to (-1, -21), (-3, -7), (-7, -3), (-21, -1) are the negative pair factors of 21.
Prime Factors of 21
It is well known that 21 has prime factors, and it is a composite number. Let’s see what those factors are.
- To begin, divide 21 by the smallest prime number, i.e., 2.
21 ÷ 2 = 10.5
In other words, 2 cannot be a factor of 21 because factors should be whole numbers. Therefore, we will proceed to the following prime number, i.e., 3.
21 ÷ 3 = 7
Therefore, 3 is one of the prime factors of 21.
You can now divide 7 by the prime numbers.
7 ÷ 2 = 3.5
7 ÷ 3 = 2.333
7 ÷÷ 5 = 1.4
7 ÷ 7 = 1
- In the division process, we received number 1, which means we cannot move forward.
In other words, the prime factors of 21 are 3 and 7, whereas 2 and 7 are prime numbers, respectively.
According to principle, we can factorize 21 as 3 × 7.

Notables:
Here are a few facts about 21:
- There are four factors in 21.
- The sum of all the factors of 21 is 32.
- When all factors of 21 are added together, the sum equals the square of 21 or 21 times 21.
| Links Related to Factors | |
| Composite Factors of 24= 1, 2, 3, 4, 6, 8, 12, and 24. | Factors of 36= 1, 2, 3, 4, 6, 9, 12, 18, and 36. |
| Factors of 48= 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | Composite Factors of 57= 1, 3, 29, and 57. |
| Factors of 42= 1, 2, 3, 6, 7, 14, 21, and 42. | Factors of 60= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. |
| Factors of 35= 1, 5, 7, and 35. | Factors of 72= 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72. |
| Factors of 84= 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84. | Composite Factors of 22= 1, 2, 11, and 22. |
Solved Examples
Example1:
Calculate the common factors of 120 and 22.
Solution:
There are 120 factors: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120.
Composite Factors of 22= 1, 2, 11, and 22.
As a result, 120 and 22 share common factors of 1 and 2.
Example 2:
Calculate 120 and 57’s common factors.
Solution:
Factors of 62 = 1, 2, 31, and 62.
Composite Factors of 57= 1, 3, 29, and 57.
Thus, the common factor of 120 and 57 is 1 and 3.
Example 3:
Calculate the common factors of 120 and 24.
Solution:
The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 and 120
Therefore, the common factors of 24 are 1, 2, 3, 4, 6, 12, and 24.
FAQs
Can you tell me the multiples and factors of 21?
Among the multiples of 21, there are 21, 42, 63, 84, 105, 126, 147, 168, 189, 210, etc.
21 has the factors 1, 3, 7, and 21.
How many multiples of 21 are there?
21, 42, 63, 84, 105, 126, 147, 168, 189, 210, … are all multiples of 21.
Can you tell me the factors of 21 and 24?
21 has the factors 1, 3, 7, and 21.
24 has the following factors: 1, 2, 3, 4, 6, 8, 12, and 24.
Does 21 only have 2 factors?
Other than 1 and 21, the number 21 has 2 more factors: 1, 3, 7, and 21.
What are the three numbers that make 21?
As an example, we have multiple sets of three numbers that add up to 21 as follows:
6, 7, 8 (6 + 7 + 8 = 21)
3, 8, 10 (3 + 8 + 10 = 21)
Get Factors of More Numbers Here
Factors of 23= 1, 23
Factors of 24=1, 2, 3, 4, 6, 8, 12, and 24.
Factors of 27=1, 3, 9, and 27.
Factors of 28=1, 2, 4, 7, 14, and 28.
Factors of 30=1, 2, 3, 5, 6, 10, 15 and 30.
