Factors of 81 – Prime Factorization & Easy Devision

Contents
Factors of 81
Factors of 81 are the numbers that, when multiplied together, give the result of 81.
As an example, the factor pair of 7 would be (1,7) and (-1,-7). If we multiply a pair of negative factors, the result will give us the original number. For example, if we multiply -1 * -7, we get 7.
Therefore, we can take into account both positive and negative factors of 7. The factor pairs of the number 81 are the whole numbers that may be positive or negative, but not fractional or decimal.
We will use the factorization method to determine the factors of 81.

Using the factorization method, first, consider 1 and 81 as factors and then find the other pair of factors of 81, which gives the result as an original number. In order to understand this method better, read the article below to find the factors of 81 in pairs.
In addition, the prime factors using the division method are explained below.
What are the Factors of -81?
When we multiply two numbers and get -81 as a product, those numbers are the factors of -81.
Here is the explanation:
-1 × 81 = -81
1 × -81 = -81
-3 × 27 = -81
27 × -3 = -81
-9 × 9 = -81
9 × -9 = -81
We can get -81 by having (-1, 81), (-3, 27), and(-9, 9) as a pair of factors. Similarly, we can also get -81 by having (1, -81), (3, -27), and (9, -9)as a pair of factors.
Important Facts of Factors
- The factors of a number are its exact divisors.
- 1 is a factor of all numbers.
- Factors of a number are always less than or equal to the number itself.
- In the end, the number itself is the greatest factor.
Pair Factors of 81
In order to find the factors of 81 in pairs, multiply the two numbers in a pair to get the original number as 81.
Examples of such factors are as follows:
1 × 81 = 81, (1, 81)
3 × 27 = 81, (3, 27)
9 × 9 = 81, (9, 9)
Thus, the positive pair factors are (1, 81), (3, 27), and (9, 9).
You can find the negative pair factors by following these steps
-1 × -81 = 81, (-1,- 81)
-3 × -27 = 81, (-3, -27)
-9 × -9 = 81, (-9, -9)
As a result, the negative pair factors are (-1, -81) (-3, -27), and (-9, -9).
How to calculate the Factors of 81?
Calculate the factors by following the steps below.
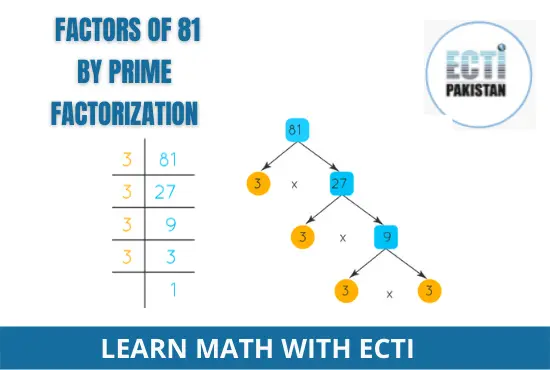
- First, write down the number 81.
- Find two numbers that produce 81 when multiplied together, such as 3 and 27, such as
3 × 27 = 81.
- As we know, 3 is a prime number that has only two factors, one and the number itself (1 and 3). Therefore, it cannot be further factorized.
3 = 3 × 1
- Look at the number 27, which is not a prime number, but a composite number. Therefore, it can be further factorized.
27 = 3 × 3 × 3 × 1
- Therefore, factorization of 81= 3 x 3 x 3 x 3 x 3 x 1
- As a final step, write down all the unique numbers you can obtain from 3 × 3 × 3 × 3 × 1.
| Factors of 81 |
| 1, 3, 9, 27, and 81 |
Prime Factors of 81 By Division Method
Number 81 must-have prime factors since it is a composite number.
Here is how to calculate the prime factors of 81.
- To begin with, divide 81 with the smallest prime number, such as 2.
81 ÷ 2 = 40.5, not a factor since it is a decimal number
- Take 81 and divide it by the next prime number, say 3.
81 ÷ 3 = 27
You can repeat the process by dividing 81 by 3.
27 ÷ 3 = 9
9 ÷ 3 = 3
3 ÷ 3 = 1
- At the end of the division process, we received number 1. Therefore, we cannot proceed further. Therefore, the prime factors are 3 * 3 * 3 * 3 or 34, where 3 represents a prime number.
| Links Related to Factors | |
| Factors of 20= 1, 3, 5, and 15. | Factors of 36= 1, 2, 3, 4, 6, 9, 12, 18, and 36. |
| Factors of 48= 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | Factors of 18= 1, 2, 3, 6, 9 and 18. |
| Factors of 24= 1, 2, 3, 4, 6, 8, 12, and 24. | Factors of 25= 1, 5, and 25. |
| Factors of 50= 1, 2, 3, 6, 7, 14, 21, and 42. | Factors of 60= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. |
| Factors of 35= 1, 5, 7, and 35. | Factors of 27= 1, 3, 9, and 27. |
| Factors of 84= 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84. | Factors of 56= 1, 2, 4, 7, 8, 14, 28 and 56. |
Find some other factors of numbers:
Factors of 20
Factors of 20 which are prime number= 1, 3, 5, and 15
Factors of 84
Factors of 84= 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.
Factors of 24
Factors of 24 which are prime number= 1, 2, 3, 4, 6, 8, 12, and 24.
Factors of 50
Factors of 50 which are prime number= 1, 2, 3, 6, 7, 14, 21, and 42.
Factors of 57
Factors of 57= 1, 3, 19, and 57.
FAQs
Is 6 a factor of 81 yes or no?
The factors of 81 are 1, 3, 9, 27, and 81, so 6 is not a factor of 81.
What are the factors of 81 and 90?
Factors of 81 = 1, 3, 9, 27, and 81
Factors of 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
What is the GCF of 81 and 88?
Prime factorization of 81= 3 × 3 × 3 × 3
Prime factorization of 88= 2 × 2 × 2 × 11
What are all the factors of 80?
Factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
What are the factors of 200?
Factors of 200 = 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100 and 200.
