Factors of 92 | with Easy division and prime factorization

Contents
Factors of 92
The factors of 92 are the real numbers that can totally divide the original number.
The factor n divides 92 into equal parts. As an example, if 7 is the factor of 21, then 21 divided by 7 equals 3. Therefore, 7 divides 21 into three equal parts. Furthermore, we need to note that the result of division leaves no remainder, and the quotient produced is a whole number.
21 ÷ 7 = 3 [Remainder = 0 and quotient = 3]
Similarly, the factors of 92 divide it equally. Let us calculate the factors as well as pair factors and prime factors.

What are the Factors of -92?
When we multiply two numbers, and we get -92 as a product, those numbers are the factors of -92.
Here is the explanation:
-1 × 92 = -92
1 × -92 = -92
-2 × 46 = -92
2 × -46 = -92
-4 × 23 = -92
4 × -23 = -92
We can get -92 by having (-1, 92), (-2, 46), and(-4, 23), as a pair of factors. Similarly, we can also get -92 by having (1, -92), (2, -46), and(4, -23), as a pair of factors.
How to Find Factors of 92?
The factors of 92 are integers that divide the original number evenly. 92 has more than two factors since it is a composite number. As a result, 92 can be divided into equal parts by all the factors.
We can find the factors by dividing 92 by the smallest natural number, i.e., 1.
92 ÷ 1 = 92
92 ÷ 2 = 46
92 ÷ 4 = 23
92 ÷ 23 = 4
92 ÷ 46 = 2
92 ÷ 92 = 1
Therefore, factors 92 are 1, 2, 4, 23, 46, and 92.
Pair Factors of 92
The original number will be the product of the pair factors. So, we need to multiply two such factors to get the pair factors of 92, whose product is 92.
1 × 92 = 92
2 × 46 = 92
4 × 23 = 92
Thus, the pair factors are (1, 92), (2, 46), and (4, 23).
Here we have the positive pair factors. Similarly, we can take into account negative pair factors that will result in the original number.
-1 × -92 = 92
-2 × -46 = 92
-4 × -23 = 92
Thus, the negative pair factors are (-1, -92), (-2, -46) and (-4, -23).
Prime Factorization of 92
In prime factors of 92, the original number is divided into equal parts. The prime factorization method can be used to determine these numbers.
As a result of prime factorization, we have to divide 92 by the prime number until we get 1.
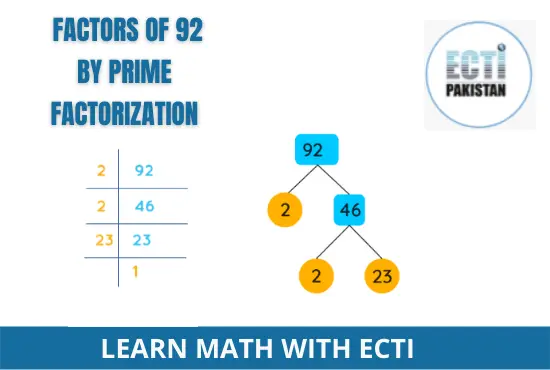
Step 1:
Since 92 is an even number, it can be divided by the smallest prime number, 2.
92/2 = 46
Step 2:
Again, 46 is an even number and is divisible by 2.
46/2 = 23
Step 3:
The prime number 23 is divisible only by 23, so it is a prime number.
23/23 = 1
Therefore,
| Prime factorization of 92 = 2 × 2 × 23 = 22 × 23 |
Solved Examples
Q.1: There are 92 apples in a basket. Nisha wants to divide these apples and put them into 4 separate baskets. How many apples does each basket hold at the end?
Solution:
Given,
Number of apples= 92
Number of baskets = 4
Number of apples in each basket = 92/4 = 23
Q.2: Find the sum of all the factors of 45 and 99.
Solution:
Factors of 45 = 1, 3, 5, 7, 15, and 35.
All Factor of 99 = 1, 3, 9, 11, 33, and 99.
Therefore, 153 is the required sum.
Q.3: What is the greatest common factor between 42 and 92?
Solution:
Both numbers have factors, so let’s write them down.
All Factor of 42 = 1, 2, 3, 6, 7, 14, 21, and 42.
92 → 1, 2, 4, 23, 46, and 92.
Therefore, the greatest common factor is 2.
Q.4: Calculate the common factors of 92 and 24.
Solution:
Factors of 92 = 1, 2, 4, 23, 46, and 92.
Find the prime factors of 24 = 1, 2, 3, 4, 6, 8, 12, and 24.
As 71 is a prime number, the common factor of 92 and 24 is 1, and 2 only.
| Link Related Factors | ||
| Factors of 30 = 1,2,3,5,6,10,15 and 30. | All factor of 24 = 1, 2, 3, 4, 6, 8, 12 and 24. | Prime factorization of 34 = 1,2, 17, and 34. |
| Factors of 36 = 1,2,3,4,6,9,12,18, and 36. | Factors of 38= 1, 2, 19, 38. | All Factor of 42 = 1, 2, 3, 6, 7, 14, 21, and 42. |
| Factors of 45 = 1, 3, 5, 9, 15, and 45. | Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | Factor of 46 = 1, 2, 23, and 46. |
| Factors of 50 = 1, 2, 5, 10, 25, 50. | Factors of 54 = 1, 2, 3, 6, 9, 18, 27 and 54. | All Factor of 99 = 1, 3, 9, 11, 33, and 99. |
FAQ`s
1. What are the factors of 92?
There are six factors of 92, which are 1, 2, 4, 23, 46, and 92.
2. What are the multiples of 92?
The first ten multiples of 92 are 92, 184, 276, 368, 460, 552, 644, 736, 828 and 920.
3. Is 92 a prime or composite?
92 has more than two factors, making it a composite number.
4. What is 92 as a product of primes?
Prime factorization of 92 = 2 × 2 × 23 or 22 × 23
5. The product of which two factors produce 92?
There are three pair factors that produce 92: (1, 92), (2, 46), and (4, 23).
6. What is the GCF of 92 and 23?
The GCF for 92 and 23 is 23.
23 → 1, 23
92 → 1, 2, 4, 23, 46, 92
Therefore, 23 and 92 have the greatest number of shared factors.
