Factors Of 9 – With Easy Division and Prime Factorization

Contents
Factors of 9
Factors of 9 are the numbers that divide it without any reminder. There are three factors in total. It has 9 as the biggest factor while 1, 3, and 9 are positive factors of 9. The sum of all factors of 9 is 13 along with (1, 9) and (3, 3) as its factors in pairs.
Fact About Factors of 9
- Factors of 9: 1, 3 and 9
- Negative Factors of 9: -1, -3 and -9
- Prime Factors of 9: 3
- Prime Factorization of 9: 3 × 3 = 32
- Sum of Factors of 9: 13
What are Factors of 9?
We can classify the factors of 9 into the two following groups:
- Positive Factors of 9
- Negative Factors of 9
Let’s explore the positive factors first.
- Positive Factors of 9
There are three positive factors of 9. All divide 9 evenly without leaving any remainder. As we know, 1 is the factor of all numbers except zero. The factors of an even number will consist of even numbers and similarly, the factors of an odd number will consist of odd numbers.
To continue, when we divide 9 by 3, it divides evenly without leaving any remainder. It means that 3 is a factor of 9.
Therefore, the factors of 9 are 1, 3, and 9.
- Negative Factors of 9
There are also three negative factors of 9. All divide 9 evenly without leaving any remainder.
Therefore, the negative factors of 9 are -1, -3, and -9. When we multiply two negative numbers, the result as a product comes in positive.
For example
-1 x -9 = 9
-3 x -3 = 9
Therefore -1, -3, and -9 are the negative factors of 9.
How to Calculate the Factors of 9?
We can calculate the factors of 9 by the following two methods:
- By Division Method
- By Prime Factorization
By using the division method, we can find factors of the numbers that divide 9 exactly without leaving a remainder.
1- Factors of 9 by Division Method
To find the prime factors of 9 by the division method, we will divide 9 by 1 to make a start and the process will go on up to 9. It is important to understand that all the factors will be smaller or equal to 9. The factors must divide evenly and there shouldn’t be any reminders left.
9 ÷ 1= 9 Divides evenly, a perfect factor
9 ÷ 2 =4.5 Fractional valuer can’t be a factor
9 ÷ 3 =3 Divides evenly, a perfect factor
9 ÷ 4 =2.25 Fractional valuer can’t be a factor
9 ÷ 5 =1.8 Fractional valuer can’t be a factor.
9 ÷ 6 =1.5 Fractional valuer can’t be a factor
9 ÷ 7 =1.28 Fractional valuer can’t be a factor
9 ÷ 8 =1.125 Fractional valuer can’t be a factor
9 ÷ 9 = 1 Divides evenly, a perfect factor
Therefore, the factors of 9 are 1, 3, and 9.
2- Factors of 9 by Prime Factorization
The second way is to find the factors through prime factorization. By this method, we divide 9 by prime numbers and check if there is no remainder. We continue by dividing by the quotient. As a result, 9 is expressed as a product of its prime factors. Factor trees can be used to determine these prime factors.
Prime Factorization of 9 by Division Method
The number 9 is divided by the smallest prime number, which divides 9 without leaving any remainder. The quotient thus obtained is then divided by the smallest or second-smallest prime number, and the process continues till the quotient is equal to 1.
Divide 9 by the prime number 3:
9 ÷ 3 = 3
As 3 is the smallest odd prime number, we can’t divide it further.
Therefore, here, the factors of 9 are 3 and 9.
Prime factorization of 9 is 9 = 3 × 3.
We must keep in mind that 3 is the only prime factor of 9.
Prime Factorization of 9 by Factor Tree Method
The root of our factor tree is 9 since we need to find the prime factors of 9. Hence, each pair of factors becomes a branch of 9.
Let us see what a factor tree of 9 looks like:
The prime factor is 3. Therefore, this is the end of the factor tree, so here, the prime factorization of 9 is 3 × 3.
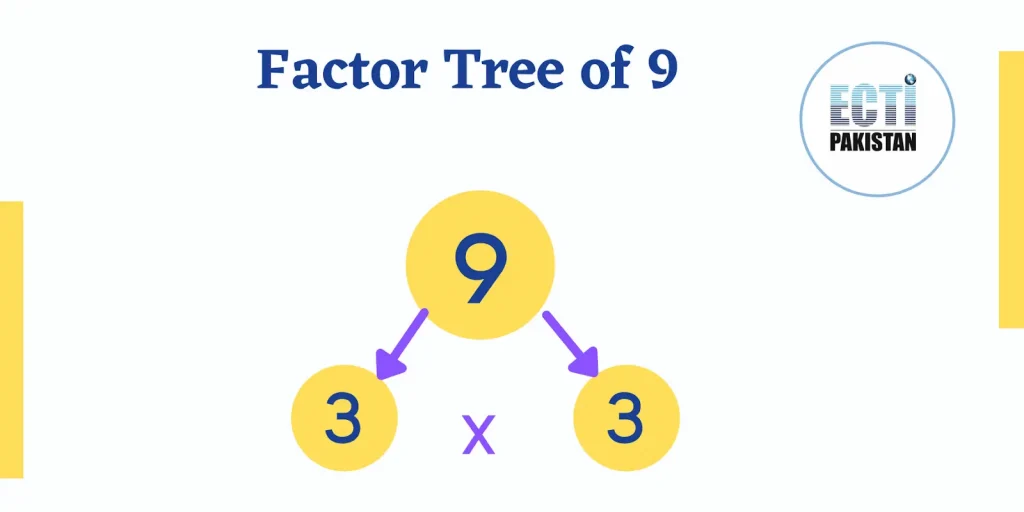
Factors of 9 in Pairs
A pair factor is the product of two numbers multiplied together. There are two types of pairs here:
- Positive pairs
- Negative Pairs
Positive Pairs:
The positive pair factors of 9 are as follows:
- 1 × 9 = 9 as a pair (1, 9)
- 3 × 3 = 9 as a pair (3, 3)
Negative Pairs:
The negative pair factors of 9 are as follows:
- -1 × -9 = 9 as a pair (-1, -9)
- -3 × -3 = 9 as a pair (-3, -3)

Important Notes:
- Factors of 9 are 1, 3, and 9.
- 1 is a universal factor of all numbers except 0.
- Factors of an odd number will consist of odd numbers.
- Factors of an even number will consist of even numbers.
- All the factors of a number will be less than or equal to the number for whom we want to find the factors.
Factors of -9
Similarly, we can find the factors of -9 by the above methods:
-1 x 9 = -9
-3 x 3= -9
3 x -3 = -9
1 x -9 = -9
We can also make the pairs as factor pairs of -9 as follows:
(-1, 9), (-3, 3), (3, -3) and (-9, 1).
Using examples and illustrations, explore the following factors:
Factors of 24
All Factors of 24= 1, 2, 3, 4, 6, 8, 12, and 24.
Factors of 49
The factors of 49 are 1, 7, and 49.
Factors of 96
The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96.
All Factors of 81= 1, 3, 9, 27, and 81.
All Factors of 53= 1 and 53.
Factors of 900
The factors of 900 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450, 900.
| Links Related to Factors | |
| All Factors of 24= 1, 2, 3, 4, 6, 8, 12, and 24. | Factors of 36= 1, 2, 3, 4, 6, 9, 12, 18, and 36. |
| Factors of 48= 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. | Factors of 18= 1, 2, 3, 6, 9 and 18. |
| All Factors of 45= 1, 2, 3, 6, 7, 14, 21, and 42. | Factors of 60= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. |
| Factors of 35= 1, 5, 7, and 35. | All Factors of 81= 1, 3, 9, 27, and 81. |
| Factors of 84= 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84. | Factors of 50= 1, 2, 5, 10, 25, 50. |
FAQs
What are the Factors of 9?
Factors of 9 are 1, 3, 9 and its negative factors are -1, -3, -9.
What is the Greatest Common Factor of 9 and 7?
Factors of 9: 1, 3, 9
Factors of 7: 1, 7. 9
1 is the only greatest Common Factor (GCF) between 9 and 7. Therefore, 9 and 7 are co-prime.
Hence, the Greatest Common Factor (GCF) of 9 and 7 is 1.
What is the Sum of the Factors of 9?
The sum of factors of 9 is 13 because 1 + 3 + 9 = 13. As we know, factors 9 are 1, 3, and 9.
What are the Prime Factors of 9?
3 is the only prime factor of 9.
How Many Factors of 9 are also common to the Factors of 3?
Factors of 9:1, 3, and 9
Factors of 3: 1, 3.
Therefore, [1, 3] are the common factors of 9 and 3
